В линейной алгебре определи́тель (или детермина́нт) — это скалярная величина, которая может быть вычислена и поставлена в однозначное соответствие любой квадратной матрице. Определитель матрицы А обозначается как
det
(
A
)
{\displaystyle \det(A)}
,
|
A
|
{\displaystyle |A|}
или
Δ
(
A
)
{\displaystyle \Delta (A)}
.
Определитель квадратной матрицы
A
{\displaystyle A}
размеров
n
×
n
{\displaystyle n\times n}
, заданной над коммутативным кольцом
R
{\displaystyle R}
, является элементом кольца
R
{\displaystyle R}
, вычисляемым по формуле, приведённой ниже.
Он «определяет» свойства матрицы
A
{\displaystyle A}
. В частности, матрица
A
{\displaystyle A}
обратима тогда и только тогда, когда её определитель является обратимым элементом кольца
R
{\displaystyle R}
.
В случае, когда
R
{\displaystyle R}
— поле, определитель матрицы
A
{\displaystyle A}
равен нулю тогда и только тогда, когда ранг матрицы
A
{\displaystyle A}
меньше
n
{\displaystyle n}
или когда системы строк и столбцов матрицы
A
{\displaystyle A}
являются линейно зависимыми.
Содержание 1 История
2 Определения 2.1 Через перестановки
2.2 Аксиоматическое построение (определение на основе свойств) 3 Значение определителя матрицы 3.1 Матрицы 2 x 2
3.2 Матрицы 3 x 3
3.3 Матрицы N × N
3.4 Альтернативные методы вычисления 4 Основные свойства определителей 4.1 Определитель как функция строк (столбцов) матрицы
4.2 Определитель и ориентированный объём
4.3 Разложение определителя по строке/столбцу и обращение матриц
4.4 Решение систем линейных алгебраических уравнений с помощью определителей
4.5 Критерий полноты и линейной независимости системы векторов
4.6 Некоторые специальные свойства определителей 5 Алгоритмическая реализация
6 Специальные виды определителей
7 См. также
8 Примечания
9 Литература
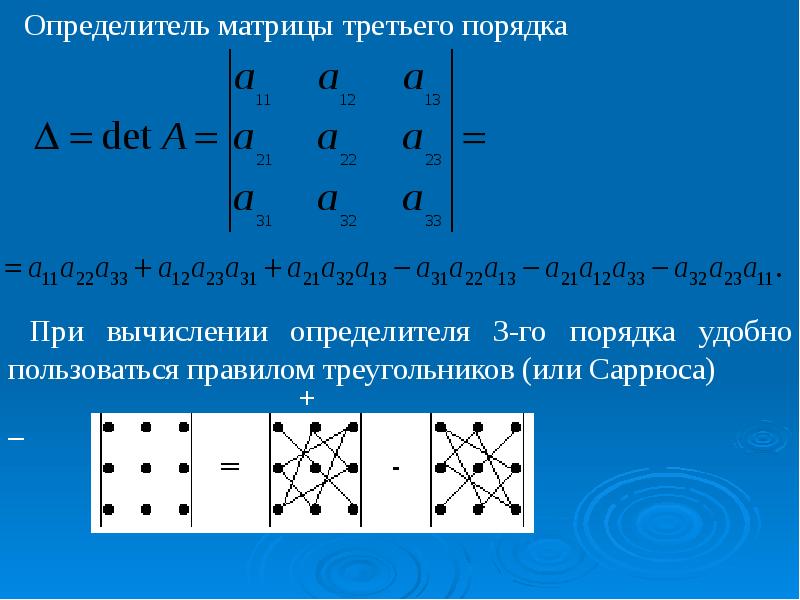
Особенности вычисления определителя матрицы